兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
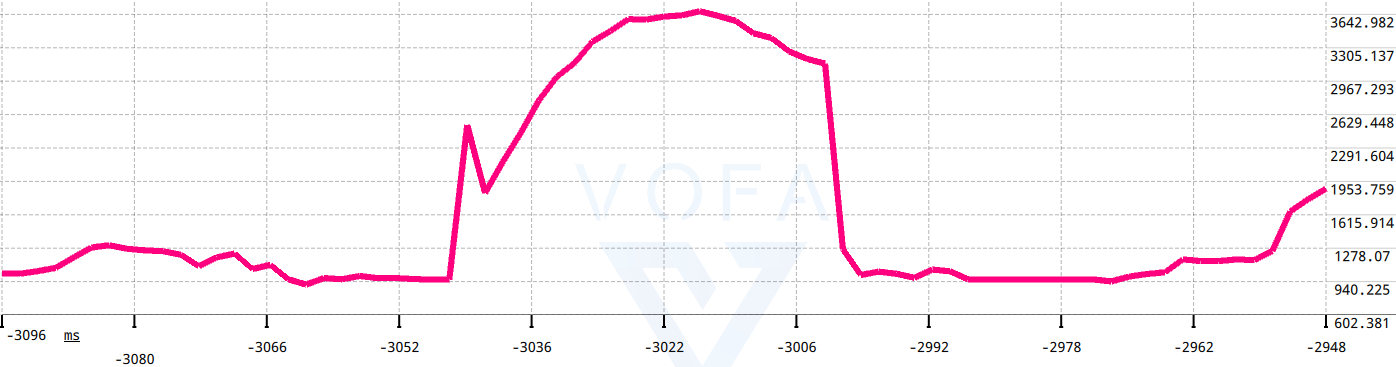
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。
兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。

从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。

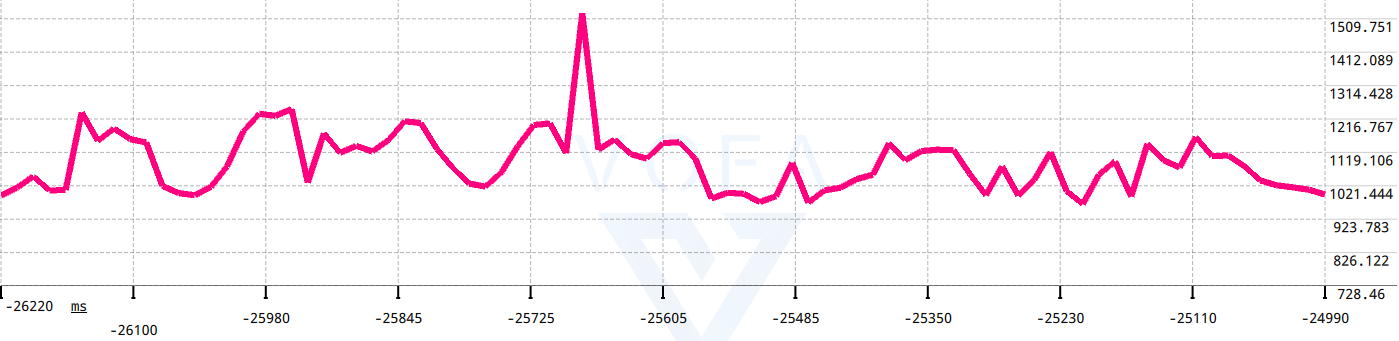
从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
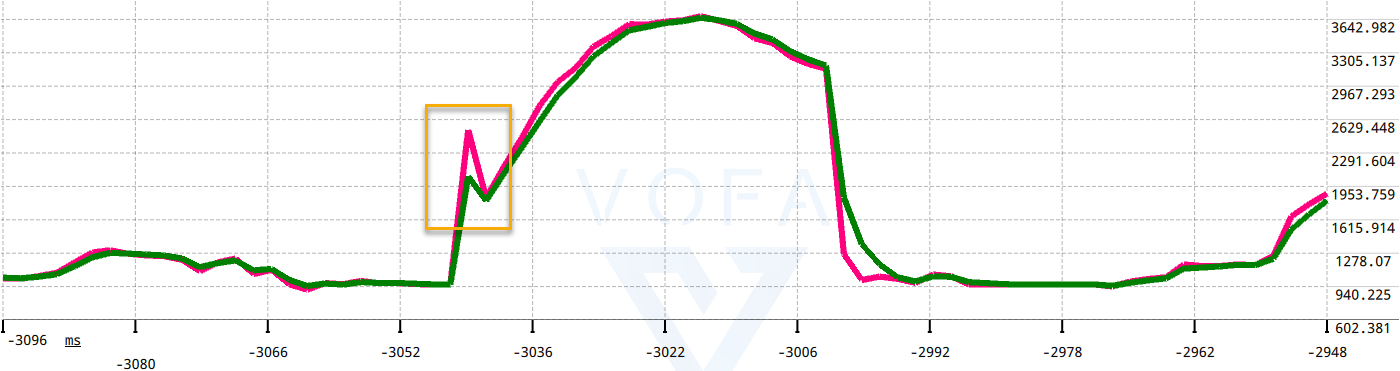
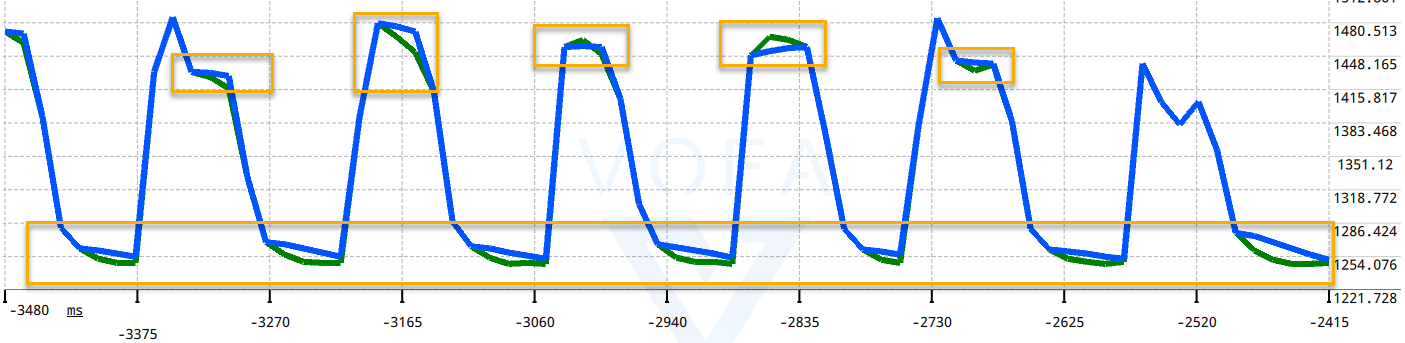
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。

从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
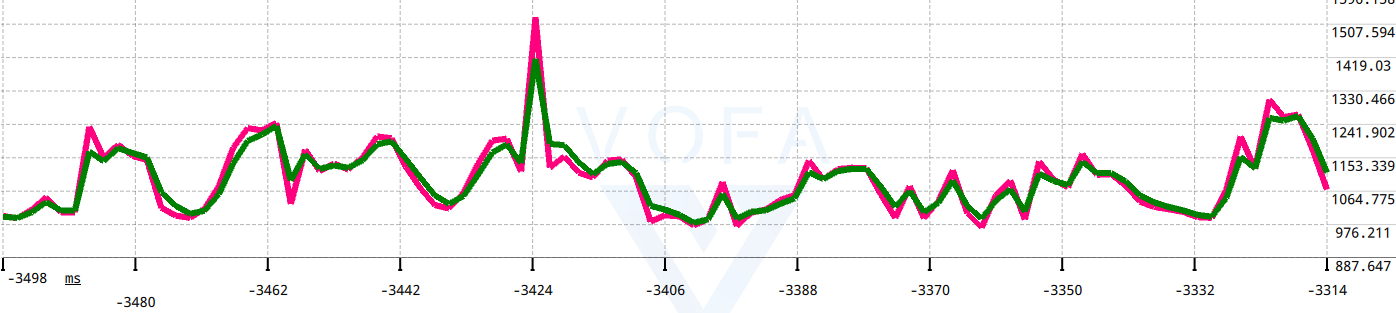
绿色为滤波后的曲线。

从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
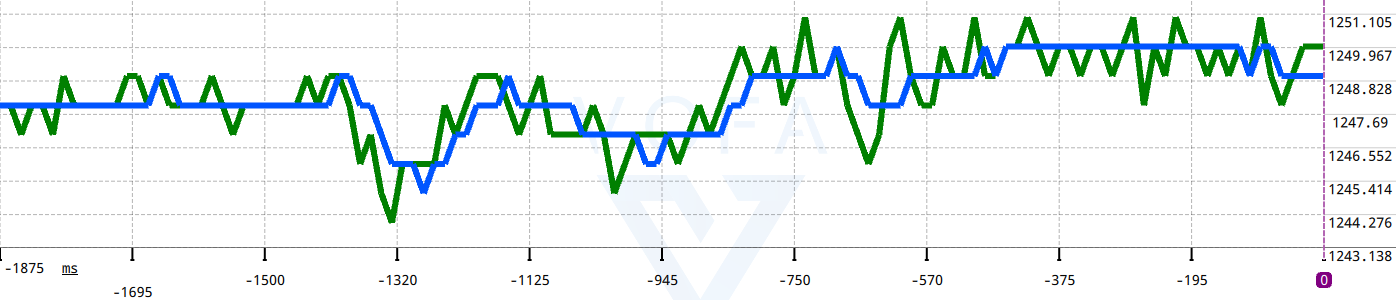
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
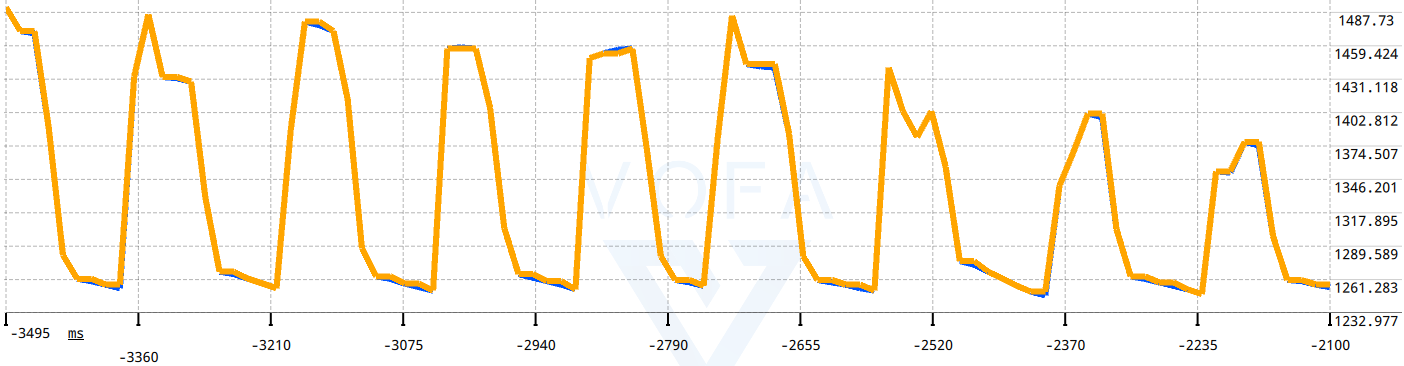
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
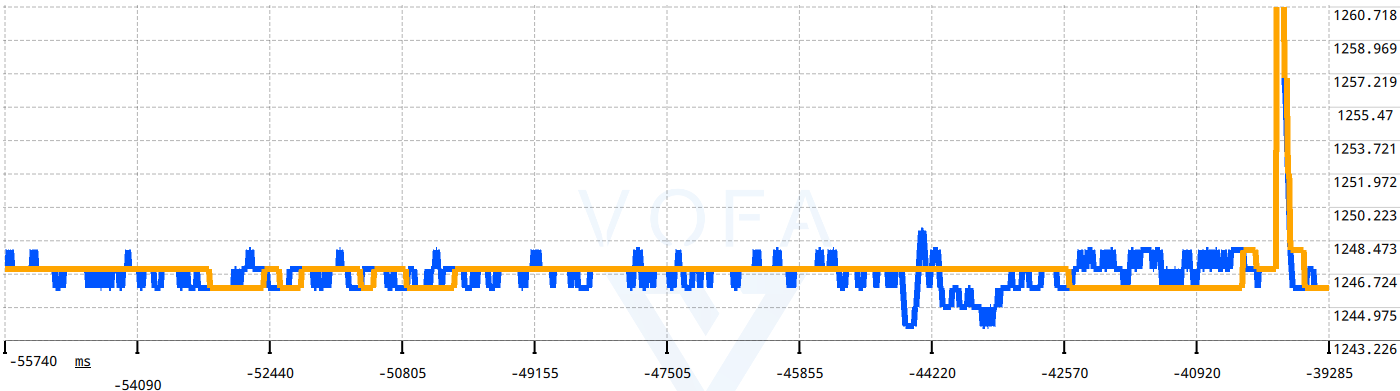
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。
从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。
兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。

从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。

从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。

从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
绿色为滤波后的曲线。

从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。
从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。
兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。

从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。

从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。

从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
绿色为滤波后的曲线。

从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。
从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
绿色为滤波后的曲线。
兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。

从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。

从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。

从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
绿色为滤波后的曲线。

从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。
从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。
兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。

从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。

从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。

从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
绿色为滤波后的曲线。

从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。
可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。
兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。

从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。

从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。

从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
绿色为滤波后的曲线。

从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。
从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。
兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。

从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。

从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。

从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
绿色为滤波后的曲线。

从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。
从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。
兼顾动静特性的ADC采样滤波
前言:
嵌入式开发中ADC是十分常用的外设,常见运用比如电量检测、温度检测、压力检测等。ADC采样易收到较多干扰导致采样不准,比如ADC时钟不准、参考电压不准、被测电压存在漂移等,这时候可通过软件算法滤波,降低噪声干扰。
1 原始波形分析
选择什么滤波算法和被滤数据特性及性能需求有关,不可脱离实际。
最近的项目开发中遇到要求ADC采样值稳定时波动要尽可能小,动态时又要能实时跟上原始数据即滞后小的需要。实际采集绘制了原始数据波形,并不理想。

从上图可观察出,当压力瞬时增大时,采样值变化出现了明显的毛刺噪声(实际该过程中不应该出现采样值回落的现象)。为了防止干扰程序运行结果,必须将毛刺减弱甚至消除。

从上图可观察出,被采集对象无变化时,理论上采样值应该为恒定的一条直线,但实际采样值还存在波动。为了防止干扰程序运行结果,必须使静态的采样值更加平稳,这样才能准确的区分出动态和静态变化,才能提高识别动态变化的精度。
2 加权滤波消除毛刺
可以通过加权滤波来消除ADC采样过程中的毛刺噪声。其算法原理如下。
$$
Q(n) = a_0 P(n) + a_1 P(n - 1) + a_2 P(n - 2) + a_3 P(n - 3)
$$
- Q(n): 表示滤波结果;
- a1~3: 表示常量系数(表示百分比,和为1)。推荐的一套参数为(0.7,0.15,0.1,0.05),含义为最近四次采样值的权重占比,权重越偏向新数据实时性越好,越偏向历史数据稳定性越好,而稳定性和实时性难以兼得;
- P(n-0~3): 表示历史采样值,P(n)表示当前采样值,P(n-1)表示上一次采样值;
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #ifndef WT_FLT_PKT_MAX_AMT
#define WT_FLT_PKT_MAX_AMT 4u
#endif
STDynaAvgFltPkt g_stDynaAvgFltPkt = {.byAmt = 5u, .awDat = {0u, 0u, 0u, 0u, 0u}, .wDynaThr = 10u};
typedef struct WtFltPkt
{
Byte byAmt;
float afWt[WT_FLT_PKT_MAX_AMT];
Word awDat[WT_FLT_PKT_MAX_AMT];
}STWtFltPkt;
STWtFltPkt g_stWtFltPkt = {.byAmt = 4u, .afWt = {0.7f, 0.15f, 0.1f, 0.05f}, .awDat = {0u, 0u, 0u, 0u}};
void MovArr(Word* pwArr, Byte byAmt, Word wDat, Bool bDir)
{
Byte byi = 0u;
if(bDir)
{
for(byi = byAmt - 1u; byi > 0u; byi--)
{
pwArr[byi] = pwArr[byi - 1u];
}
pwArr[0u] = wDat;
}
else
{
for(byi = 0u; byi < byAmt - 1u; byi++)
{
pwArr[byi] = pwArr[byi + 1u];
}
pwArr[byAmt - 1u] = wDat;
}
}
float CalcWtFlt(STWtFltPkt* const cpstWtFltPkt, Word wDat)
{
float fRes = 0.0f;
Byte byi = 0u;
MovArr(cpstWtFltPkt->awDat, cpstWtFltPkt->byAmt, wDat, TRUE);
for(byi = 0u; byi < cpstWtFltPkt->byAmt; byi++)
{
fRes += cpstWtFltPkt->afWt[byi] * cpstWtFltPkt->awDat[byi];
}
return fRes;
}
|
2.1 加权滤波处理动态
通过加权滤波后得到的曲线如下图所示,绿色为滤波后的曲线。

从波形可看出,滤波后的曲线有效的消除了采样值急速上升过程中的毛刺噪声,是的曲线变化更平滑。由于参数配比增加了稳定性因此实时性变差,波形出现滞后现象,实际使用中可调节权重系数的配比从而达到一个适中的值。
2.2 加权滤波处理静态
绿色为滤波后的曲线。

从波形可看出,滤波后的曲线可以有效过滤毛刺噪声并且增加稳定性,可调节权重系数的配比从而达到一个适中的值。
3 动态平均滤波
常规的平均滤波优缺点很明显,由于平均滤波的特性使得滤波后数据很慢才能达到波峰波谷处,在坡度处(上升坡度或下降坡度)也会变得比实际平缓很多。优点是静态情况下波形可变得显著稳定。因此为了使用平均滤波的静态特性,但是又保证动态情况下的实时响应,我们选择性的使用平均滤波,即在波形动态变化时不进行平均滤波,波形处于静态情况下时进行平均滤波。这种根据动静态实时调节的平均滤波我这里姑且将其称为动态平均滤波。
判断动静态的方法很简单,原理通过判断曲线变化的斜率,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #ifndef AVG_FLT_PKT_MAX_AMT
#define AVG_FLT_PKT_MAX_AMT 5u
#endif
typedef struct DynaAvgFltPkt
{
Byte byAmt;
Word awDat[AVG_FLT_PKT_MAX_AMT];
Word wDynaThr;
}STDynaAvgFltPkt;
float CalcDynaAvgFlt(STDynaAvgFltPkt* const cpstDynaAvgFltPkt, Word wDat)
{
DWord dwSum = 0.0f;
Byte byi = 0u;
float fRes = 0.0f;
MovArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, wDat, TRUE);
if(Abs(cpstDynaAvgFltPkt->awDat[0u], cpstDynaAvgFltPkt->awDat[1u]) >= cpstDynaAvgFltPkt->wDynaThr)
{
SetArr(cpstDynaAvgFltPkt->awDat, cpstDynaAvgFltPkt->byAmt, cpstDynaAvgFltPkt->awDat[0u]);
fRes = (float)cpstDynaAvgFltPkt->awDat[0u];
}
else
{
for(byi = 0u; byi < cpstDynaAvgFltPkt->byAmt; byi++)
{
dwSum += cpstDynaAvgFltPkt->awDat[byi];
}
fRes = (float)dwSum / cpstDynaAvgFltPkt->byAmt;
}
return fRes;
}
|
3.1 动态平均滤波处理动态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

可以看到使用动态滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此实时性完全没有问题,但坡度较为平缓小于阈值时,平均滤波使得波形进一步变缓,这是副作用但其影响可控。
3.2 动态平均滤波处理静态
以下为滤波效果。绿色为被滤波形(加权滤波输出),蓝色为动态平均滤波结果。

从波形可看出,静态下使用平均滤波将有效增加波形稳定度,消除小幅度抖动。
4 施密特滤波
经过动态平均滤波后静态下的波形稳定性得到较大提升,单波形仍然在小幅度的上下波动,为了消除这些小幅度的高频抖动噪声可以使用施密特滤波(姑且这么命名吧)。但是为了不影响动态特性,该算法依然需要判断动静状态,仅在静态下起作用。
施密特滤波的原理很简单,通过斜率区分动静态,实际代码中可判断最近两次采样的差值是否大于阈值,这个阈值需根据实际调试确定。当判为动态时不进行滤波,当判为静态时对一定范围内的波动记录连续出现次数,累积到一定次数后才修改值,从而达到“确认”的目的实现迟滞效应。
以下是代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
typedef struct SmtFltPkt
{
Word wRefVal;
Word wSusVal;
Word wRng;
Word wRptCnt;
Word wUpdThr;
}STSmtFltPkt;
STSmtFltPkt g_stSmtFltPkt = {.wRefVal = 0u, .wSusVal = 0u, .wRng = 3u, .wRptCnt = 0u, .wUpdThr = 10u};
Word CalcSmtFlt(STSmtFltPkt* const cpstSmtFltPkt, Word wDat)
{
Word wDevAbs = 0u;
wDevAbs = Abs(cpstSmtFltPkt->wRefVal, wDat);
if(wDevAbs <= cpstSmtFltPkt->wRng)
{
if(wDat == cpstSmtFltPkt->wSusVal)
{
cpstSmtFltPkt->wRptCnt++;
if(cpstSmtFltPkt->wRptCnt >= cpstSmtFltPkt->wUpdThr)
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wRefVal = cpstSmtFltPkt->wSusVal;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
}
}
else
{
cpstSmtFltPkt->wRptCnt = 0u;
cpstSmtFltPkt->wSusVal = wDat;
cpstSmtFltPkt->wRefVal = wDat;
}
return cpstSmtFltPkt->wRefVal;
}
|
4.1 施密特滤波处理动态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可以看到使用施密特滤波算法后,在波形大于阈值的坡度处不进行动态平均滤波,因此保证了实时性。
4.2 施密特滤波处理静态
以下为滤波效果,蓝色为被滤波形(动态平均滤波输出),橙色为施密特滤波结果。

从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。
从波形可看出,静态下使用施密特滤波波形的稳定度已经变得非常平稳,几乎完全消除小幅度抖动。