第九章——数据结构与算法
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
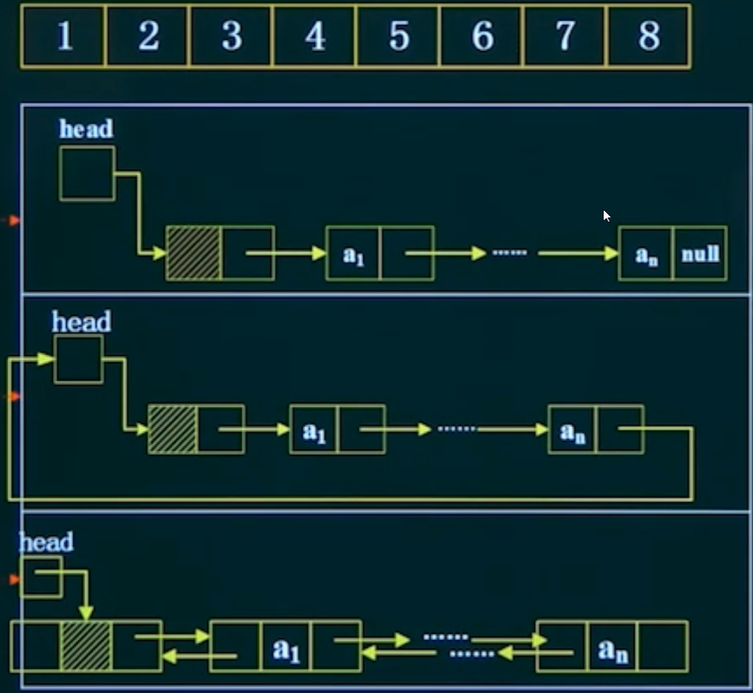
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
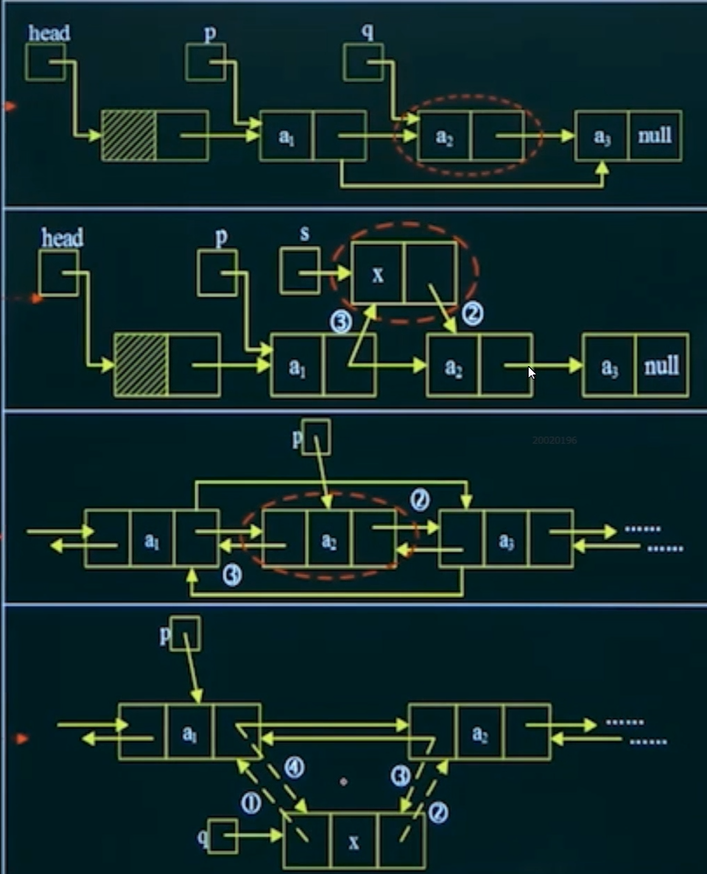
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
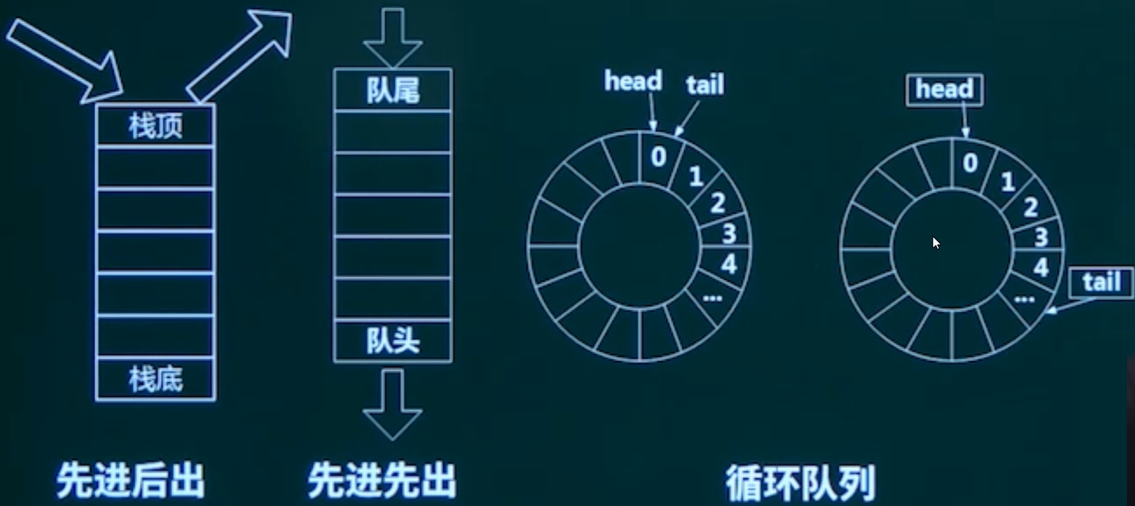
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
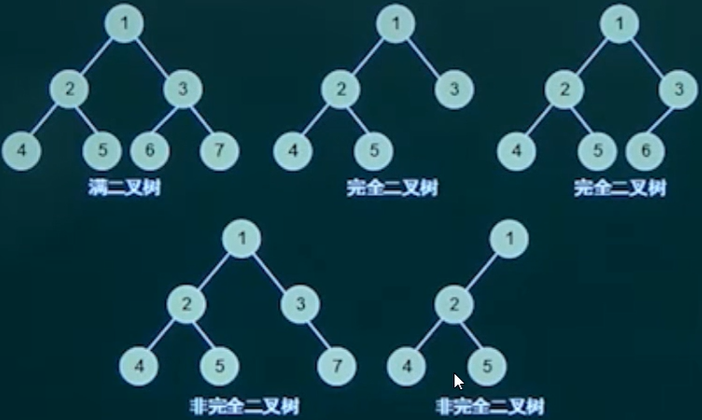
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
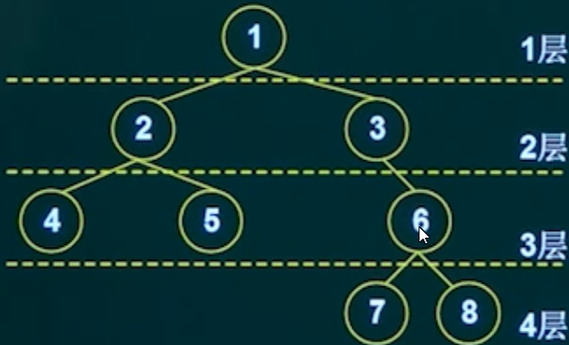
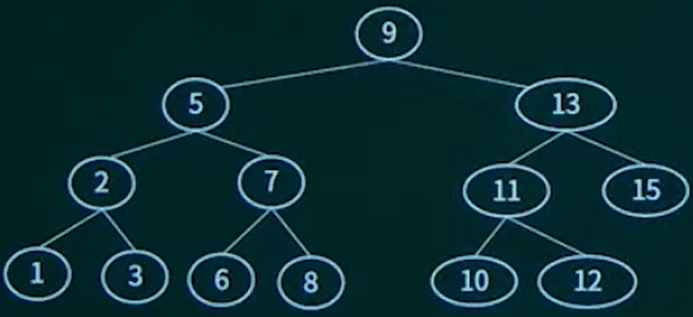
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
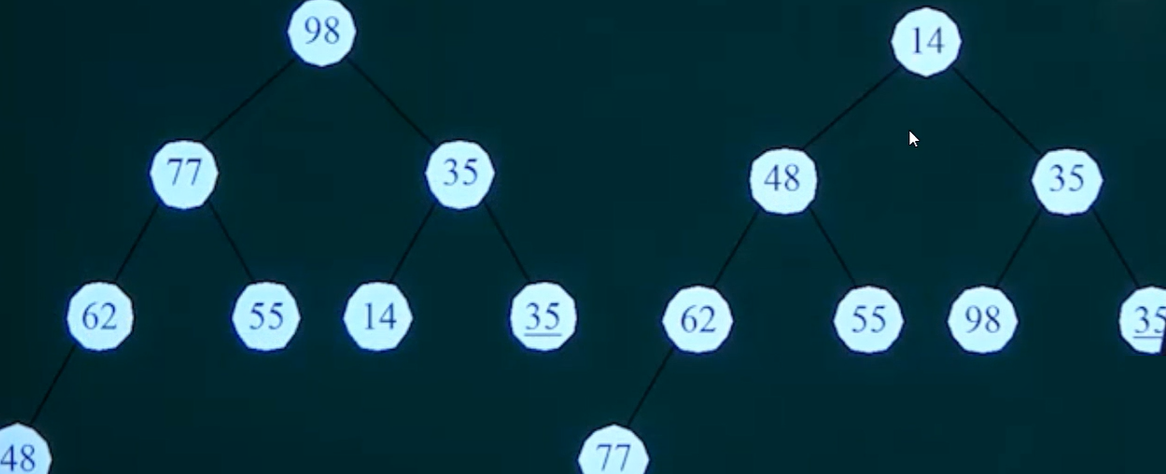
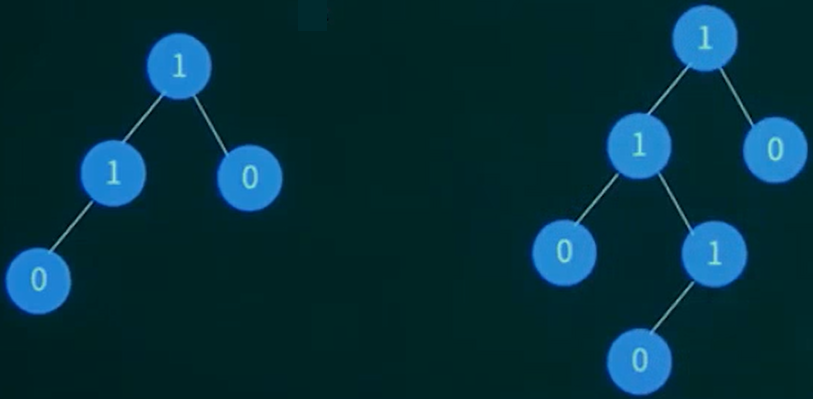
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
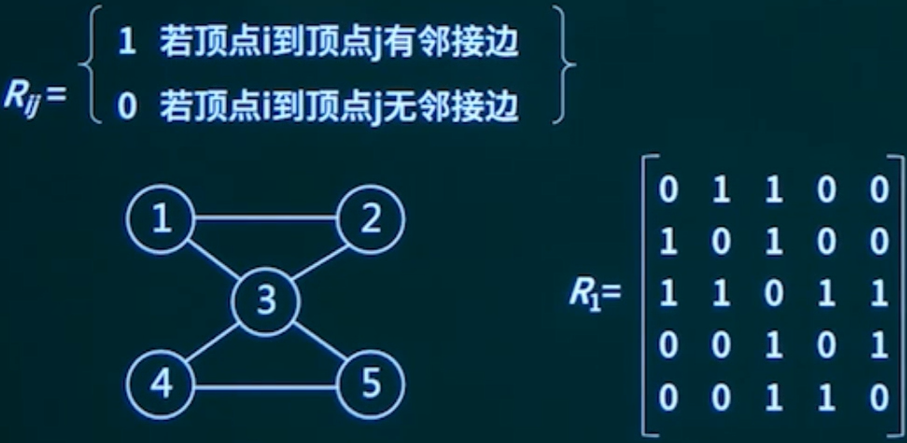
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
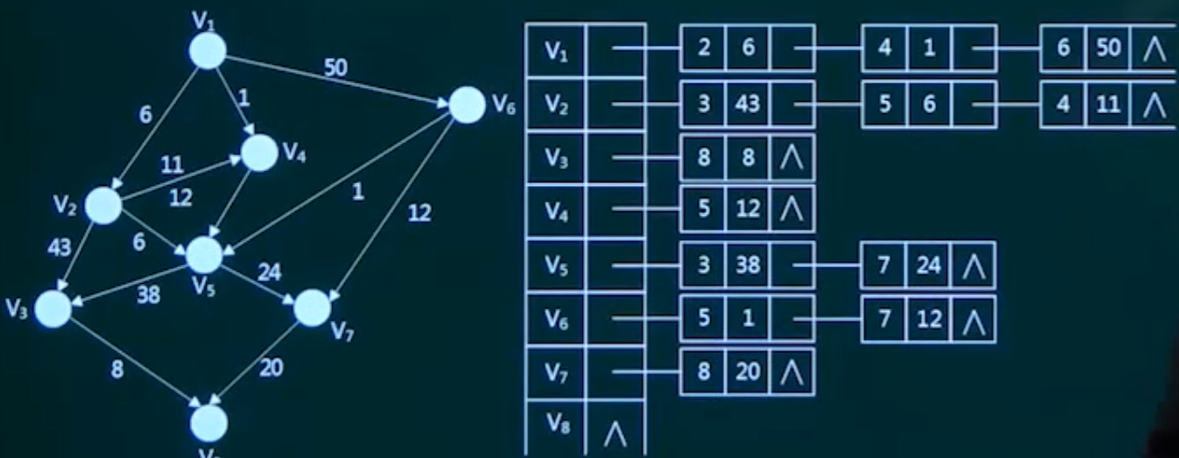
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
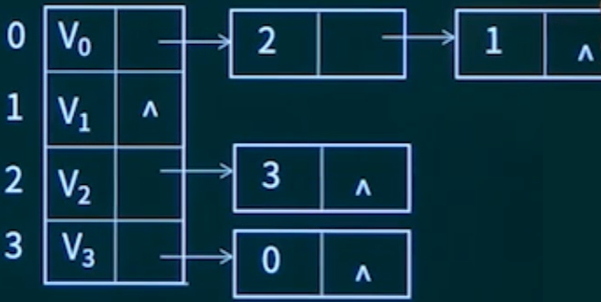
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
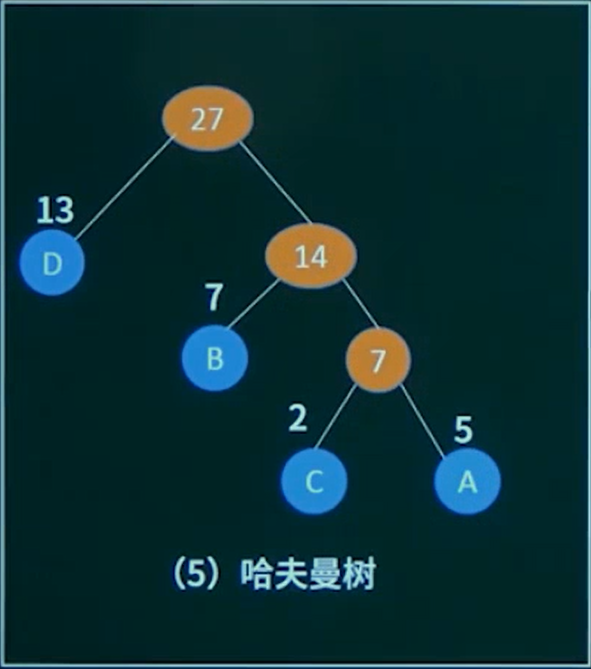
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
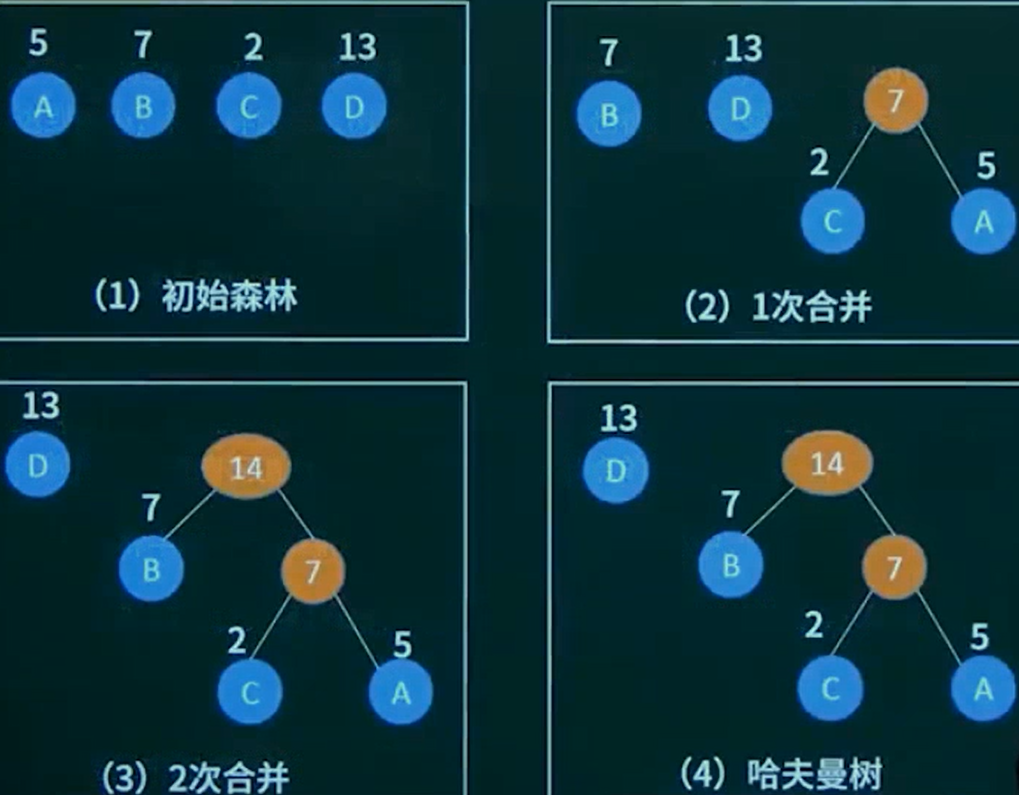
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
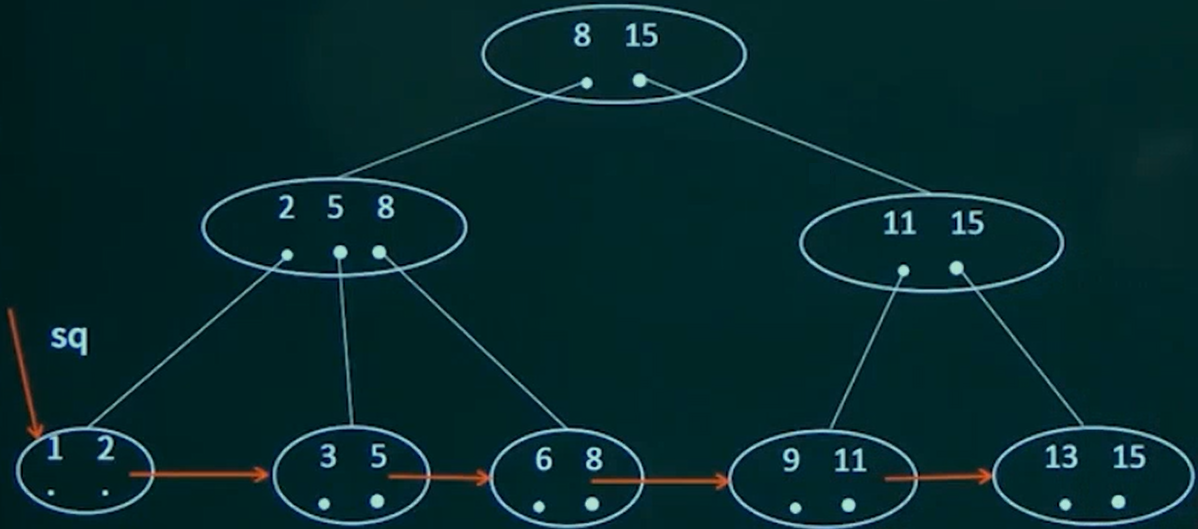
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
11.3 图的遍历
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
第九章——数据结构与算法
前言:
计算机第九章节主要知识点。
1 知识点介绍
- 数据结构与算法概念
- 线性表
- 数组与矩阵
- 树与二叉树
- 图
- 查找
2 数据结构定义
- 数据结构
- 数据逻辑结构:指数据元素之间的管理。
- 线性结构:一对一关系
- 非线性结构:一对多,多对多关系
- 数据物理结构:数据在物理设备上具体如何存储。
- 数据逻辑结构:指数据元素之间的管理。
3 算法概念
算法的5个重要特征
- 又穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须由确切的含义,不能含糊不清。
- 输入(>= 0)
- 输出(>= 1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限此后得到确定的结果,例如a = 0,b / a就无效。
4 伪代码
伪代码是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现。
5 线性表
5.1 线性表的概念
常见线性表的两种存储结构。
- 顺序存储结构(如:顺序表)
- 链式存储结构(如:链表)
逻辑上连续,物理上不一定连续。
- 顺序表:随机存取。查询和修改容易,元素插入和删除麻烦,需要移动元素。
- 链表
- 单链表
- 循环链表
- 双向链表
5.2 链表基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
5.3 例题
- 以下关于单链表存储结构特征的叙述中,不正确的是(D)。
A. 表中结点所占用存储空间的地址不必是连续的
B. 在表中任意位置进行插入和删除操作都不用移动元素
C. 所需空间与结点个数成正比
D. 可随机访问表中的任一结点
5.4 队列和栈
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序。
5.5 例题
- 令序列X、Y、Z的每个元素都按顺序进栈,且每个元素进栈和出栈仅一次,则不可能得到的出栈序列是(C)。
A. XYZ
B. XZY
C. ZXY
D. YZX
6 广义表
广义表示n个表元素组成的有限序列,是线性表的推广,通常用递归的形式进行定义,记作: $LS = (a_0, a_1, …, a_n)$
注:其中LS是表名, $a_i$ 是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n = 0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
例,有广义表LS1 = (a, (b, c), (d, e)),其长度为?深度为?
答案:长度为3,深度为2。
7 串
串是仅由字符构成的有限序列,是取值范围受限的线性表,一般记为 S = ‘a1a2…an’,其中S是串名,单引号括起来的字符序列是串值。
8 数组
二维数组分按行存储和按列存储。c/c++的多维数组是按行、连续存储逇。FORTRAN语言,Matlab中,数组按列优先顺序存储。
| 数组类型 | 存储地址计算 |
|---|---|
| 一维数组a[n] | a[i]的存储地址为:a + i * len |
| 二维数组a[m][n] | a[i][j]的存储地址(按行存储)为:a + (i * n + j) * len a[i][j]存储地址(按列存储)为:a + (j * m + i) * len |
8.1 例题
- 数组a[1 … n, 1 … m](n > 1, m > 1)中的元素以行为主序存放,每个元素占用1个存储伟,则数组元素a[i, j] $(1 \leq i \leq n, 1 \leq j \leq m)$ 相对于数组空间首地址的偏移量为(A)
A. (i - 1) * m + j - 1
B. (i - 1) * n + j - 1
C. (j - 1) * m + i - 1
D. (j - 1) * n + i - 1
- 若二维数组arr[1 … M, 1 … N]的首地址为base,数组元素按列存储且每个元素占用K个存储单元,则元素arr[i, j]在该数组空间的地址为()。
A. base + ((i - 1) * M + j - 1) * K
B. base + ((i - 1) * N + j - 1) * K
C. base + ((j - 1) * M + i - 1) * K
D. base + ((j - 1) * N + i - 1) * K
9 树与二叉树
- 结点的度
- 树的高度
- 叶子结点
- 分支结点
- 内部结点
- 父结点
- 子结点
- 兄弟结点
- 层次
二叉树的重要特征。
- 在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i \geq 1)$ ;
- 深度为k的二叉树最多有 $2^k - 1$ 个结点 $(k \geq 1)$ ;
- 对任何一颗二叉树,如果其叶子结点数为 $n_0$ ,度为2的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$ 。
- 如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到 $log_2n + 1$ 层,每层从左到右),则对任一结点i $(i \geq i \geq n)$ ,有
- 如果i = 1,则结点i无父结点,是二叉树的根;如果i > 1,则父结点是i / 2;
- 如果2i > n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2i + 1 > n,则结点i无右叶子结点,否则,其右子结点是结点2i + 1;
9.1 二叉树遍历
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 层序遍历
前序遍历:12457836,中序遍历:42785136,后序遍历:48752631,层次遍历:12345678。
10 堆
堆是计算机科学中的一类特殊的数据结构的统称。堆通常是一个可以被看做一颗完全二叉树的数组对象。
若n个元素的序列 ${a_1, a_2 … a_n}$ 满足
则分别称该序列 ${a_1, a_2, … a_n}$ 为小根堆和大根堆。
从堆的定义可以看出,对实质是满足如下性质的完全二叉树:
- 二叉树中任一非叶子结点均小于(大于)它的孩子结点。
- 堆总是一颗完全二叉树。
例如:下面序列为堆,对应的完全二叉树分别为。
1 | 98 77 35 62 55 14 35 48 |
10.1 例题
- 对于n个元素的关键字序列 ${k_1, k_2, … k_n}$ ,当且仅当满足关系 $k_j \leq k_{2i}$ 且 $k_i \leq k_{2i + 1}$ {i = 1.2…[n/2]}时称其为小根堆(小顶堆)。以下序列中,(D)不是小根堆。
A. 16, 25, 40, 55, 30, 50, 45
B. 16, 40, 25, 50, 45, 30, 55
C. 16, 25, 39, 41, 45, 43, 50
D. 16, 40, 25, 53, 39, 55, 45
11 图
11.1 图的存储
11.1.1 邻接矩阵表示法
邻接矩阵表示法用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素 $R_{ij}$ 定义为。
为无向图。表示稀疏矩阵时空间浪费大。
11.1.2 邻接链条表示法
首先把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
11.2 例题
- 某有向图G的邻接表如下图所示,可看出该图中存在弧 $<v_2, V3>$ 而不存在从顶点 $V_1$ 出发的弧。以下关于图G的叙述中,错误的是()。
A. G中存在回路
B. G中每个顶点的入度为1
C. G的邻接矩阵是对称的
D. 不存在弧 $V_3, V_1>
11.3 图的遍历
12 查找算法
- 五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
- 顺序表查找
12.1 顺序查找
顺序查找的过程:将待查找的关键字可key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功,否则返回失败。顺序查找主要针对少量的、无规则的数据。
1 | 4 7 10 18 30 2 46 24 15 |
12.2 二分查找
二分法查找的基本过程是:(设R[low, …, high]是当前的查找区)
- 确定该区间的中间位置:mid = [(low + high) / 2],向下取整。
- 将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key > k,则由表的有序性可知R[mid, …, n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low, …, mid -1]中。因此,新的查找区间是左子表R[low, …, high],其中high = mid - 1.
- 若R[mid].key < k,则要查找的k必在mid的右子表R[mid + 1, …, high]中,即新的查找区间是右子表R[low, …, high],其中low = mid + 1。
- 若R[mid].key = k,则查找成功,算法结束。
- 下次查找是针对新的查找区间进行,重复步骤(1)和(2)。
- 在查找过程中,low逐步增加,而high逐步减少。如果high < low,则查找失败,算法结束。
12.3 二叉查找树(排序)
二叉查找树的定义:二叉排序树或者是一颗空树,或者是具有如下特性的二叉树。
- 若它的左子树不空,则左子树上所有节点的值均小于根节点的值。
- 若它的有子树不空,则右子树上所有节点的值均大于根节点的值。
- 它的左、右子树也都分别是二叉排序树。
对二叉查找树进行中序遍历,即可得到有序的序列。
查找过程:二叉查找(排序)树是先对待查找的数据进行生成树,确保数的左分支值小于右分支的值,然后再去和每个结点的父结点比较大小,查找最合适的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建数。
具体步骤为。
- 若查找的关键字等于根节点的关键字,查找成功。
- 若查找的关键字小于根节点的关键字,递归查找左子树。
- 若查找的关键字大于根节点的关键字,递归查找右子树。
- 若子树为空,则查找不成功。
12.4 二叉平衡树
定义:又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树或右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
平衡因子。
二叉树上任一结点的左子树深度减去右子树深度的差值,称为此结点的平衡因子。
12.5 例题
- 关于二叉排序树的说法,错误的是(C)。
A. 对于二叉排序树进行中序遍历,必定得到结点关键字的有序序列
B. 依据关键字无序的序列建立二叉排序,也可能构造出单支树
C. 若构造二叉排序树时进行平衡化处理,则根节点的左子树结点数与右子树结点数的差值一定不超过1
D. 若构造二叉排序树时进行平衡化处理,则根结点的左子树高度与右子树高度的差值一定不超过1
12.5 哈夫曼树
定义:给定N个权值作为N个叶子节点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的数,权值较大的结点离根较近。
一般可以按下面步骤构建。
- 将所有左、右子树都为空的作为根节点。
- 在森林中选取两棵根节点的权值最小的数作为一棵新树的左、右子树,且置新树的附加根节点的权值为其左、右子树上根结点的权值之和。
- 从森林中删除这两棵树,同时把新树加入到森林中。
- 重复2、3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
应用场景:对字符集中的字符进行编码和译码。
12.6 例题
- 以下有关哈夫曼树的说法中,错误的是(C)。
A. 哈夫曼树又被称为最优二叉树
B. 哈夫曼树是一种带权路径长度最短的树
C. 具有n个叶子结点的权值为 $W_1, W_2, …, W_n$ 的最优二叉树是唯一的
D. 哈夫曼树可以用来进行通信电文的编码和解码
13 B树
B树,有时又写为B-树或B_树(其中的“-”或者“_”只是连字符,并不读作“B减树”)。一颗m阶的B树是一颗平衡的多路搜索树,它或者是空树,或者是满足下列性质的树。
- 树中每个结点至多有m棵子树。
- 若根结点不是叶子结点,则至少有两棵子树。
- 除根之外的所有非终端结点至少有[m/2](向上取整)棵子树。
- 所有的非终端结点中包含下列信息数据:
$(n, A_0, K_1, A_1, K_2, A_2, …, K_n, A_n)$ ,其中: $K_i (i = 1, 2, …, n)$ 为关键字,且 $K_i < K_{i + 1}$ (i = 1, …, n - 1)。
$A_i (i = 0, …, n)$ 为指向子树根结点的指针,且指针 $A_{i -1}$ 所指子树中所有结点的关键字均小于 $K_i(i = 1, …, n)$ , $A_n$ 所指子树中所有结点的关键字均大于 $K_n$ , $n ([m / 2] - 1 \leq n \leq m - 1)$ 为关键字的个数(或n + 1为子树个数)。其中[m / 2]表示向上取整。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
14 B+树
是B-树的一种变型,一个m阶的B+树具有如下几个特征。
- 每个叶子结点中含有n个关键字和n个指向记录的指针,并且所有叶子节点彼此相链接构成一个有序链表,其头指针指向含最小关键字的节点。
- 每个非叶子节点中的关键字 $K_i$ 即为其相应指针 $A_i$ 所指子树中关键字的最大值。
- 所有叶子节点都处在统一层次上,每个叶子节点中关键字的个数均介于[m / 2](向上取整)和m之间。
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)
15 散列表
散列表构造的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0 .. n - 1](n << m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:假设有一个大小为7的表,现在要将(13, 18, 19s, 50, 20, 27)散列到表中。
- 选择散列函数,例如使用hash(x) = x % 7作为散列函数。
- 计算数据散列值,并放到合适的位置。
| 哈希地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 关键码 | 50 | 18 | 19 | 13 |
地址重复时出现冲突,即散列冲突。
15.1 解决散列冲突
- 链地址法(拉链法)
- 开放地址法
$H_i = (Hash(key) + d_i) % m$ i = 1, 2, …, k $(k \leq m - 1)$
其中Hash(key)为哈希函数,m为哈希表的表长,di为增量序列。常见的增量序列有三种。
- di = 1, 2, 3, …, m - 1,称为线性他侧再散列。
- di = $1^2, {-1}^2, 2^2, {-2}^2, 3^3, …, ±k^2$ ,称为二次探测再散列。
- di = 伪随机数列,称为随机探测再散列,如:di = Random(key)。
15.2 例题
- 用哈希表存储元素时,需要进行冲突(碰撞)处理,冲突是指(B)。
A. 关键字被依次映射到地址编号连续的存储位置
B. 关键字不同的元素被映射到相同的存储位置
C. 关键字相同的元素被映射到不同的存储位置
D. 关键字被映射到哈希表之外的位置
16 总结
考查形式主要是概念区分以及部分计算题型,主要出现在上午的选择题当中。
- 树的遍历
- 图的遍历
- 典型的时间复杂度
需要记忆。
- 数据结构与算法的概念
- 线性表(顺序表、链表、栈、队列)
- 数组与矩阵
- 图
- 树与二叉树
- 查找(二分查找、哈希)