主动笔的曲线校准方法

前言：
  为了保证主动笔的书写体验，减小每一支笔之间的压力感知差异，在主动笔出货前一般会有一个校准过程。校准是指主动笔的压力曲线校准，这条压力曲线横轴是笔尖的克重压力，纵轴是输出到显示屏的压力等级。校准的目的就是保证随便拿一直笔，相同的力去书写使其粗细变化都是基本一致的。

1 主动笔的压力曲线

1.1 什么样的压力曲线适合主动笔呢？

很容易想到随着克重压力的增加，输出的压力等级也应该增加，也即压力和压力等级是正相关关系。那么更具体的曲线趋势应该是哪种呢？我们讨论如下三种：

• 指数函数关系；
• 一次函数关系（属于幂函数）；
• 对数函数关系；

1.2 指数函数关系

  这里以指数函数$$p=ae^{bg}+c$$举例说明，g是克重反应压力大小，p是压力等级。我们假设主动比在克重400g时达到最大压力等级4095，0克重时对应压力等级为0。我们假设300g时压力等级为1586。拟合出的压力曲线公式为：$$p=117e^{\frac{g}{111.62213}}+117$$。
  我们使用python3画出这条曲线：

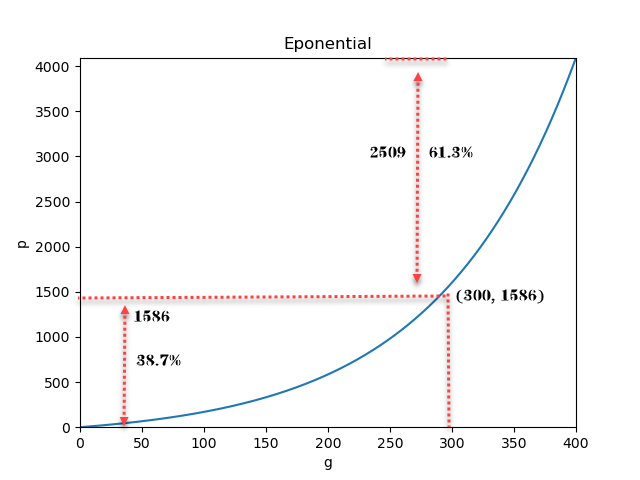
指数函数式压力曲线，38.7%的压力等级划分给300g以下，61.3%划分给300g以上。这样的曲线书写缺点如下：

• 按书写习惯，正常书写下对笔尖的压力主要分布在100~250g之间，而此曲线100~250g之间压力等级变化幅度太小，导致书写粗细变化不明显。
• 100~250g的压力等级都低于1000，导致写出的曲线整体偏细。
• 300g以下压力等级只占38.7%，且这1586的压力等级上升缓慢，300g以上压力等级占61.3%，且这2509的压力等级上升迅速，书写起来会感觉书写力量稍小时笔迹较细，一用力笔迹就变很粗，书写效果出现两个极端。

  python绘图代码如下：

import numpy as np
import math
import matplotlib.pyplot as plt

x = np.arange(0.0001, 400, 0.0001)

y = [117 * math.exp(a / 111.62213) - 117 for a in x]

plt.plot(x, y)
plt.xlabel("g")
plt.ylabel("p")
plt.xlim(0, 400)
plt.ylim(0, 4095)
plt.title("Eponential")
plt.show()

1.3 一次函数关系

  比较容易先想到的就是呈直线关系的一次函数，它将压力等级和克重均匀分配。我们这里以一次函数$$p=kg+b$$举例说明，该曲线过点(0, 0)，(400, 4095)。拟合出曲线公式为：$$p=\frac{4095}{400}g$$。
我们使用pathon3画出这条曲线：

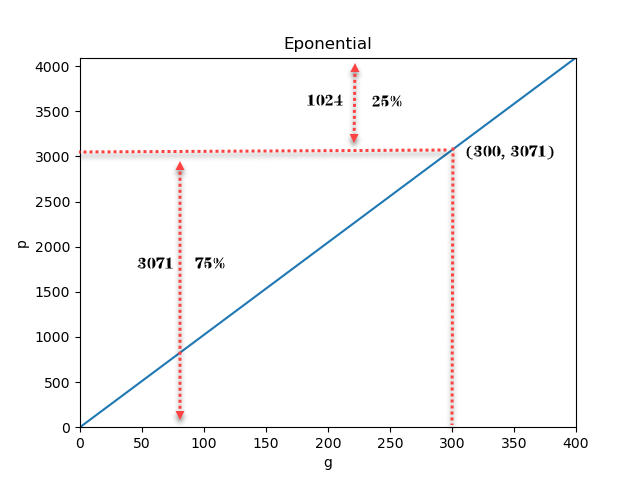
  一次函数式压力曲线，75%的压力等级划分给300g以下，25%划分给300g以上。相比较指数函数式压力曲线，  它将更多的压力等级划分给书写更为常用的压力克重下。这样的曲线书写缺点如下：

• 我们可以将0~400g的克重分段来看，0~50g的小克重在书写中的体验经常是一闪而过的。0~100g主要用于进行轻描淡绘时，按照人的习惯，使用的力越大对力的精细度控制就越难，使用的力越小越能更精细的控制力度也即粗细，我们可以考虑给0~100g分配更多的压力等级让人去控制。而300g以上在书写中也较少达到，在对笔进行点击操作或持续的擦除操作时可能才会容易达到，但这些情况并不关心压力大小，可以继续减小300g之后的压力分配。
• 一次函数中100g时对应的压力等级为1024笔迹还是偏细，300g时的压力等级为3071，跨度比较大，粗细变化对大多数用户来说还是太过明显。

  python绘图代码如下：

import numpy as np
import math
import matplotlib.pyplot as plt

x = np.arange(0.0001, 400, 0.0001)

y = (4095 / 400) * x

plt.plot(x, y)
plt.xlabel("g")
plt.ylabel("p")
plt.xlim(0, 400)
plt.ylim(0, 4095)
plt.title("Eponential")
plt.show()

1.4 对数函数

  通过了上面的分析，我们对压力曲线提出如下需求：

1. 它随着压力变化有明显的粗细变化，太细太粗都不好，中等的压力等级应该分布在我们常用的克重范围附近100g~250g。
2. 100g以下的小克重，这个段可以分配多一些压力等级便于轻描时写出更多细线效果。
3. 300g以上克重使用较少，不需要在这段分配较多压力等级。
4. 压力曲线一定是平滑的曲线，不能出现阶梯变化，否则在书写中会出现粗字落差较大的笔画。
     以对数函数$$p=ae^{bx}+c$$进行曲线拟合，其过点(0, 0)，(400, 4095)，假设又经过点(100, 2728)，拟合得到曲线$$p=984.63937e^{g}-1804.43185$$
     我们使用pathon3画出这条曲线：

  以上曲线只是举例说明，曲线参数需要根据实际去调整，但大致是符合对数曲线的趋势的。

  python绘图代码如下：

import numpy as np
import math
import matplotlib.pyplot as plt

x = np.arange(0.0001, 400, 0.0001)

y = [984.63937 * math.log(a, math.e) - 1804.43185 for a in x]

plt.plot(x, y)
plt.xlabel("g")
plt.ylabel("p")
plt.xlim(0, 400)
plt.ylim(0, 4095)
plt.title("Eponential")
plt.show()

2 压力曲线校准方法

  为什么要校准曲线？所有笔不能通用一条曲线吗？
  当然不能。每支笔起始都有差异，电压的差异，传感器的差异，组装结构的差异等都会导致每支笔具有不同的压力曲线。同样的砝码100g，压在同一批生产的笔上，单片机采集到的压力采样值会各不相同。我们要让笔A知道，当它采集到采样值x1时对应的克重是100g，也要让笔B知道当它采集到采样值x2时对应的克重是100g。
通过上面分析，我们的压力曲线大致是这个样子：

  这是一条连续的曲线，让单片机去实现这样一条曲线有两种方案：

• 取离散点，构成多条首尾相接线段去粗略近似。
• 取连续曲线，给单片机曲线公式去运算。

2.1 取离散点用近似曲线

2.1.1 方法描述

  单片机的运算能力是非常有限的，特别你写小型终端设备使用的单片机更偏向于低功耗，使用其进行逻辑控制可以，一旦涉及到数学运算就非常吃力。特别有的单片机Flash也很小限制了代码量，很可能没有足够的Flash导入数学库。使用取离散点用近似曲线的方优点是计算量小。缺点也明显离散出来的曲线与原本连续平滑的曲线重合度低。重合度与取离散点个数有关，点取太多占用存储空间大且校准繁琐，对校准设备精度有要求，因此往往无法取太多的点。

  上图中选取了A、B、C、D四个点，我们连接这些离散的点，以OA、AB、BC、CD多段线段构成的曲线去近似原来的连续压力曲线。可以看出明显的重合度不太高。为什么不继续增加离散点，OA段之间为什么不多几个离散点呢？
  理论上来说是可以增加，比如达到10个离散点。0~400g有10个离散点均匀划分的话，那么每增加40g就分布一个校准点。假设是人工去放砝码增加克重，放的时候会有一个砝码的自由落体高度以及手的抖动，这些都是误差。而这些误差在0~100g段进行校准时其占比会很大，导致校不准，所以我上面在0~100g没有设计校准点。不过具体还要取决于所使用的压力传感器是否足够刚性或者说形变回复能力。比如一块海绵，你轻柔的放上100g砝码和先放400g砝码然后取走300g最终产生的形变量是不同的，跟为复杂的是相同的砝码放上去放置的时间不同，这个形变量也不同。我曾经试过用硅胶作为压感（可以看成一种压敏电阻），它就具有类似海绵的一些特性，导致曲线很难校准，不过成本会很低。如果形变回复较好，克重引起的变化稳定的的传感器可以增加多一些校准点，但是太多则生产效率会降低，想象下每一支笔要校准10个点。要求不高的情况下3~5个点就够了。

2.1.2 实际操作

  讲完方法就该讲讲如何实际操作。压力传感器一般都是输出电信号，单片机通过ADC取采集电信号大小从而知道当前克重值。所以我们放上100g砝码时会采集到对应的采样值，将这个采样值写入到Flash中保存，下次采样值又达到这个值时我们就知道时100g了。同这个办法分别记录下A、B、C、D四个点的采样值。如果采集到的采样值是介于A点和B点之间呢？因为两点可以去顶一条直线，我们有A点和B点的值就可以求出线段AB，再将采样值带入线段AB方程就能得到采样值对应的近似克重。用这个方法可以得到OA、AB、BC、CD线段的方程，也即整条压力曲线。

  c示例代码如下：

//将采样值转换为频率(定时器设置值)，分为两段直线
void GetPressureFrq_StraightLine_2(AdcSample)
{
    //采样值限幅
    uint16_t u16AdcSample = 0;
    if(AdcSample < ADC_SAMPLE_MIN)
    {
        u16AdcSample = ADC_SAMPLE_MIN;
    }
    else if(AdcSample > ADC_SAMPLE_MAX)
    {
        u16AdcSample = ADC_SAMPLE_MAX;
    }
    else
    {
        u16AdcSample = AdcSample;
    }

    //第一段直线部分，变化较快
    if(AdcSample <= ADC_SAMPLE_MIDDLE)
    {
        g_u16Temp = FRQ_MIDDLE - FRQ_MIN;
        g_u16Temp1 = ADC_SAMPLE_MIDDLE - ADC_SAMPLE_MIN;
        g_u16PressureFrqVal = (uint16_t)((uint32_t)g_u16Temp * (u16AdcSample - ADC_SAMPLE_MIN) / g_u16Temp1 + FRQ_MIN);
    }
    else//AdcSample > ADC_SAMPLE_MIDDLE 第二段直线部分，变化更缓
    {
        g_u16Temp = FRQ_MAX - FRQ_MIDDLE;
        g_u16Temp1 = ADC_SAMPLE_MAX - ADC_SAMPLE_MIDDLE;
        g_u16PressureFrqVal = (uint16_t)((uint32_t)g_u16Temp * (u16AdcSample - ADC_SAMPLE_MIDDLE) / g_u16Temp1 + FRQ_MIDDLE);
    }
}

2.2 取连续曲线

2.2.1 方法描述

  使用一些低性能的单片机进行带浮点的对数函数运算会很吃力，有些单片机直接算不出来或运算时间太长。

  如图，不能计算对数函数，那么我们就把对数函数拟合为多项式函数，将对数运算转化为指数运算。当然，过高的指数项对单片机来说运算量依旧过大，我们可以适当舍弃一些高次项，牺牲一点重合度，比如最高只取到3次项或4次项。
  对连续曲线的校准就是起始就是校准曲线公式中的参数。比如我们采样的曲线多项式为$$p=ag^{3}+bg^{2}+cg+d$$，这个公式里起主导作用的很明显是高次项，我们可以将a作为需要校准的参数确定好后写入Flash，而其他参数作为固定参数。取连续曲线的方法校准过程简单节省人力，一般只用校准一两个点即可。

2.2.2 实际操作

  比如我们将200g设定为连续曲线的校准点，放上200g砝码后可采集到对应的采样值，同时我们也知道这个采样值带入公式后计算出来的压力等级，比如为2600，然后以a作为变量将a参数从小到大或从大到小轮询尝试。当a取某值时计算出来的压力等级最接近2600时即认为此时的a为连续曲线要找的参数，将其写入Flash中。

  c示例代码如下：

//将采样值转换为频率(定时器设置值)，拟合一段曲线，强烈建议用多项式拟合避免使用math库
//此函数工作在8M时钟源下
void GetPressureFrq_CurveLine(AdcSample)
{
    g_u16PressureFrqVal = (uint16_t)(342.97471f + 0.00156f * AdcSample + g_u16FlashData[2] * 1E-8f * AdcSample * AdcSample);      //自动校准

    if(g_u16PressureFrqVal > PRESSURE_WINDOW_SCOPE_MAX)
    {
        g_u16PressureFrqVal = PRESSURE_WINDOW_SCOPE_MAX;
    }
    if(g_u16PressureFrqVal < PRESSURE_WINDOW_SCOPE_MIN)
    {
        g_u16PressureFrqVal = PRESSURE_WINDOW_SCOPE_MIN;
    }
}

3 如何给单片机程序加校准模式

  已经刷好程序的的半成品如何在出厂时能校准，到用户手上跑正常的功能？
  这其实是要求程序具有两种模式，一种是校准模式，一种是正常模式。想想Windows，在开机的时候如果按下某些按键就可以进入安全模式一个道理。在程序上电的时候单片机读取某个IO，如果这个IO口的电平是高，则进入校准模式，而正常情况下它是低，所以在用户手上它上电时监测不到高电平就自然是正常模式了。另外为了校准的结果有一些显示，还可以操作一些LED灯，串口输出一些数据灯。